zad
matthew: cześć,
mam takie zadanie
dla jakiej wartości współczynnika k rownanie x3 + kx + 2099x = 2009
spełniają trzy rózne liczby naturalne? wyznacz te liczby.
zaczałem tak:
w(1) = 1 + k + 2099 − 2009 = 0
W(1) = k = − 91
i taką też mam odpowiedź, ale gdybym jej nie miał to nie wiedziałbym, ze k = akurat − 91
prosze o pomoc, nie wiem jak inaczej mogłbym się zabrać za to zadanie...
1 kwi 14:15
matthew: potem wystarczyłoby za k wstawić luiczbe i pierwiastki byłyby do rozwiązania, ale nie wiem jak
to k inaczej obliczyc...
1 kwi 14:20
tim: Chyba x3 + kx2 + 2099x − 2009 = 0 czyż nie?
1 kwi 15:35
matthew: właśnie tak

1 kwi 17:08
Godzio:
x3 + kx2 + 2099x − 2009 = 0
x3 + kx2 + 90x + 2009x − 2009 = 0
x3 + x2(k+90 − 90) + 90x + 2009x − 2009 = 0
x3 + x2(k+90) − 90x2 + 90x + 2009x − 2009 = 0
x2(x+ k + 90) − 90x(x−1) + 2009(x−1) = 0
żeby były 3 rozwiązania musi być wspólny czynnik czyli:
k + 90 = −1
k = −91
Wydaje mi się że tak jest poprawnie
1 kwi 17:17
matthew: Mam jeszcze takie zadanie:
zbadaj przebieg zmienności funkcji f(x) = |x
2 − 6x + 8| + |x
2 − 6x + 5| i narysuj jej wykres.
Podaj liczbę pierwiastków równania f(x) = m w zależności od parametru m.
zacząłem tak:
x2 − 6x + 8 = 0
Δ = 36 − 32 = 4
√Δ = 2
x2 − 6x + 5 = 0
Δ = 36 − 20 = 16
√Δ = 4
i nie wiem.... mam dalej zrobić to w taki sposób:
x<1 1≤x<2 2≤x<4 4≤x<5 x≥5
−−−−−|
1−−−−−−−−−|
2−−−−−−−−−−−|
4−−−−−−−−−−|
5−−−−−−−> ?
1 kwi 17:22
Godzio: Raczej tak

troche bedzie liczenia
1 kwi 17:25
matthew: wiem....., bo juz próbowałem to zrobić w ten sposob , ale niestety mam błędną odpowiedz....
1 kwi 17:27
Godzio: dobra zaraz pomoge

1 kwi 17:29
matthew: poczekaj, napiszę co mi wyszło

1 kwi 17:31
matthew: I) x<1 −−−−−−> 2x2 − 12x +13
II) 1≤x<2 −−−−−−−> 3
III) 2≤x<4 −−−−−> − 2x2 + 12x − 13
IV) 4≤x<5 −−−−−−−−−−−> 2x2 − 12x + 13
V) 5≥x −−−−−−−−−> 2x2 − 12x + 13
{.....
i teraz wystarczyłoby podstawić to do f(x) = {....
{....
odpowiedź mam taką:
{2x2 − 12x + 13 dla x∊(−∞,1>∪<5,+∞)
f(x) = {3 dla x∊(1,2)∪(4,5)
{− 2x2 + 12x − 13 dla x∊<2,4>
czyli rozwiązanie jest niezgodne z moją odpowiedzia....
1 kwi 17:37
matthew: ta odpwoedz, która napisałem jest oczywiście odpowiedzią z książki....
1 kwi 17:40
matthew:  Godzio
Godzio skąd wiedziałeś, ze tak trzeba rozpisać ten przykład? można to po czymś
rozpoznać?....
nobo nie wiem... wiedziałbyś jak zrobić to zadanie, gdybyś nie znał odpowiedzi?
1 kwi 17:47
Godzio:
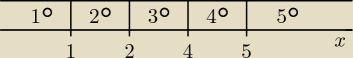
f(x) = |x
2 − 6x + 8| + |x
2 − 6x + 5|
f(x) = |(x−2)(x−4)| + |(x−1)(x−5)| = |x−2| * |x−4| + |x−1| * |x−5|
Najpierw Rysowanie wykresu :
1
o x∊(−
∞,1)
f(x) = (−x+2)(−x+4) + (−x+1)(−x+5) = x
2 −6x + 8 + x
2 − 6x + 5 =
2x2 − 12x + 13
2x
2 − 12x + 9 = 0
x
2 − 6x + 4,5 = 0
Δ = 18
| | 6 − 3√2 | |
x2 = |
| ≈ 0,87 oba nalezą do przedziału (1o i 5o) |
| | 2 | |
2
o x∊<1,2)
f(x) = (−x+2) * (−x+4) + (x−1) * (−x+5) = x
2 − 6x + 8 − x
2 + 6x − 5 =
3
brak pierwiastków
3
o x∊<2,4)
f(x) = (x−2) * (−x+4) + (x−1) * (−x+5) = −x
2 + 6x − 8 − x
2 + 6x − 5 =
−2x2+ 12x − 13
−2x
2 + 12x − 13 = 0
x
2 − 6x + 6,5 = 0
Δ = 10
| | 6 − √10 | |
x2 = |
| ≈ 1,41 oba nie należą do przedziału <2,4) |
| | 2 | |
4
o x∊<4,5)
f(x) = (x−2) * (x−4) + (x−1) * (−x+5) = x
2 − 6x + 8 − x
2 + 6x − 5 =
3
5
o x ∊<5,
∞)
f(x) = (x−2) * (x−4) + (x−1) * (x−5) = x
2 − 6x + 8 + x
2 − 6x + 5 =
2x2 − 12x + 13
{2x
2 − 12x + 13 dla x∊(−
∞,1>∪<5,
∞)
f(x) = {3 dla x∊<1,2)∪<4,5)
{−2x
2 + 12x − 13 dla x∊<2,4)
Pierwiastki:
Myślę że się zgadza dokończ to co zostało w zadaniu do zrobienia

1 kwi 17:52
Godzio:
Co do tamtego zadania : trzeba rozbijać tak żeby otrzymać wspólny czynnik który można wyciągnąć
przed nawias
1 kwi 17:53
matthew: troche sie nie zgadza.... porównaj swoj odpowiedź do tej którą podałem powyzej....
dziekuję za odpowiedzi

1 kwi 18:18
Godzio: jeśli chodzi o przedziały czy domknięty czy otwarty to bez różnicy

1 kwi 18:20
Godzio: bo można wziąść taki przedział:
(−∞,1) i <1,2) a mozna tez
(−∞,1> i (1,2)
1 kwi 18:21
matthew: mam zadanie z parametrem:
dane jest równanie: 2x
2 + (m−1)x − m
2 = 0.
wyznacz te wartości parametru m, dla których kolejne liczby: 1, suma pierwiastków, suma
odwrotności pierwiastków tego równania, tworzą ciąg geometryczny.
z delty wyszło mi, że m∊R
x
1 + x
2
prosze o pomoc
1 kwi 19:29
Godzio:
a, b, c − ciąg geometryczny => b
2 = ac
m∊R
| | 1 | | 1 | |
1 , x1 + x2 , |
| + |
| |
| | x1 | | x2 | |
| | −m+1 | | −m+1 | |
( |
| )2 = 1 * |
| / *4m2 |
| | 2 | | −m2 | |
(m
2 − 2m +1)*m
2 = 4(m−1)
m
4 − 2m
3 + m
2 = 4m − 4
m
4 − 2m
3 + m
2 − 4m + 4 = 0
m
4 − m
3 − m
3 + m
2 − 4m + 4 = 0
m
3(m − 1) − m
2(m − 1) − 4(m − 1) = 0
(m − 1)(m
3 − m
2 − 4) = 0
(m − 1) * (m−2)(m
2 + m + 2) = 0
m = 1 v n = 2
1 kwi 19:49
matthew: dzieki

a gdyby te dane tworzyły c. arytmetyczny, to jak wtedy wyglądałby wzór?
1 kwi 20:30
Godzio: | | a+c | |
a, b, c − ciąg arytmetyczny −> |
| = b => a + c = 2b |
| | 2 | |
1 kwi 20:52
matthew:
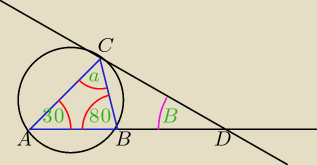
mam takie zadanie:
w okrąg wpisano trójkąt ABC, w którym |∠CAB| = 30
o i |∠ABC| = 80
o. Przez punkt C poprowadzono
styczną do okregu. Styczna ta przecina przdłużenie boku AB w punkcie D. Oblicz miarę kąta ADC.
α = 70
o
proszę o jakąś podpowiedz

1 kwi 22:02
tim: Dorysuj promienie koła.
Pamiętaj, że środek koła jest w miejscu przecięcia dwusiecznych.
1 kwi 22:05
matthew: trójkąt jest wpisany w okrąg, wiec raczej symetralne.... ale to i tak nie wiele mi pomoglo....
1 kwi 22:16
Godzio:
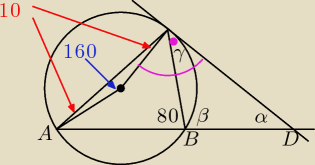
α = 180 − β − γ
β = 180 − 80
γ = 90 − (α − 10 )
wszystko zrozumiałe ?
1 kwi 22:26
Godzio:
y = 90 − (70 − 10)

1 kwi 22:30
matthew: zrozumiale jest.... prawie wszystko

skad wiesz, ze kąt równy jest 160
o?
1 kwi 22:30
Godzio: kąt środkowy oparty na tym samym łuku co kąt wpisany <B = 80o jest 2 razy większy od niego
1 kwi 22:31
matthew: aha i dlaczego odrazu przyjąłeś sobie, że tam jest kąt prosty? co to jest za własnośc?
1 kwi 22:32
Godzio: pomiędzy promieniem łączącym środek z punktem stycznosc a styczną zawsze jest kąt prosty

1 kwi 22:33
matthew: ok. zadanie zrobione
dzieki

1 kwi 22:53
matthew: Punkt A = (−2,4) należy do okręgu o równaniu x2 + y2 − 6x + 4y + c = 0
oblicz długość promienia tego okręgu.
próbowałem podstawić punkt a do wzoru na okrąg, ale wychodzi mi zły wynik....
Czy mam tutaj stworzyć układ równań z prostą przechodząca przez punkt A i S oraz wzorem na
okrąg, w celu obliczenia "c"?
prosze o jakąs wskazówkę
1 kwi 23:24
matthew: ok już nie trzeba. odwołuję pytanie ... przepraszam
zrobiłem błąd w obliczeniach
1 kwi 23:28
matthew: jest druga cześć do tego zadania...
napisz równanie stycznej do okręgu w punkcie A... tutaj nie mam zadnego pomysłu
proszę o pomoc
1 kwi 23:45
Godzio:
Ustal wzór prostej AS i znajdź prostą prostopadłą do prostej AS przechodzącą przez punkt A

dasz rade ?
2 kwi 00:05
matthew: znalazłem już wcześniej, ale okazało sie, ze to ma być jakieś równanie, a nie wzór.....
2 kwi 00:09
matthew: masz jakiś pomysł?
w odpowiedzi jest: 5x − 6y + 24 = 0
2 kwi 00:27
Godzio:
S(3,−2)
A(−2,4)
−2 = 3a + b
4 = −2a + b
−6 = 5a
prosta prostopadła:
6y = 5x + 34
5x − 5y + 34 = 0
chyba chodzi 34 a nie 24 prawda ?
2 kwi 00:56

 troche bedzie liczenia
troche bedzie liczenia


 Godzio skąd wiedziałeś, ze tak trzeba rozpisać ten przykład? można to po czymś
rozpoznać?....
nobo nie wiem... wiedziałbyś jak zrobić to zadanie, gdybyś nie znał odpowiedzi?
Godzio skąd wiedziałeś, ze tak trzeba rozpisać ten przykład? można to po czymś
rozpoznać?....
nobo nie wiem... wiedziałbyś jak zrobić to zadanie, gdybyś nie znał odpowiedzi?
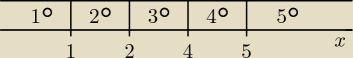 f(x) = |x2 − 6x + 8| + |x2 − 6x + 5|
f(x) = |(x−2)(x−4)| + |(x−1)(x−5)| = |x−2| * |x−4| + |x−1| * |x−5|
Najpierw Rysowanie wykresu :
1o x∊(−∞,1)
f(x) = (−x+2)(−x+4) + (−x+1)(−x+5) = x2 −6x + 8 + x2 − 6x + 5 = 2x2 − 12x + 13
2x2 − 12x + 9 = 0
x2 − 6x + 4,5 = 0
Δ = 18
f(x) = |x2 − 6x + 8| + |x2 − 6x + 5|
f(x) = |(x−2)(x−4)| + |(x−1)(x−5)| = |x−2| * |x−4| + |x−1| * |x−5|
Najpierw Rysowanie wykresu :
1o x∊(−∞,1)
f(x) = (−x+2)(−x+4) + (−x+1)(−x+5) = x2 −6x + 8 + x2 − 6x + 5 = 2x2 − 12x + 13
2x2 − 12x + 9 = 0
x2 − 6x + 4,5 = 0
Δ = 18



 a gdyby te dane tworzyły c. arytmetyczny, to jak wtedy wyglądałby wzór?
a gdyby te dane tworzyły c. arytmetyczny, to jak wtedy wyglądałby wzór?
 mam takie zadanie:
w okrąg wpisano trójkąt ABC, w którym |∠CAB| = 30o i |∠ABC| = 80o. Przez punkt C poprowadzono
styczną do okregu. Styczna ta przecina przdłużenie boku AB w punkcie D. Oblicz miarę kąta ADC.
α = 70o
proszę o jakąś podpowiedz
mam takie zadanie:
w okrąg wpisano trójkąt ABC, w którym |∠CAB| = 30o i |∠ABC| = 80o. Przez punkt C poprowadzono
styczną do okregu. Styczna ta przecina przdłużenie boku AB w punkcie D. Oblicz miarę kąta ADC.
α = 70o
proszę o jakąś podpowiedz 
 α = 180 − β − γ
β = 180 − 80
γ = 90 − (α − 10 )
wszystko zrozumiałe ?
α = 180 − β − γ
β = 180 − 80
γ = 90 − (α − 10 )
wszystko zrozumiałe ?

 skad wiesz, ze kąt równy jest 160o?
skad wiesz, ze kąt równy jest 160o?


 dasz rade ?
dasz rade ?